Objektorientierte Modellierung und Programmierung mit GLOOP
Collage
Bei der Java-Bibliothek GLOOP (Graphics Library for Object Oriented Programming) handelt es sich um eine didaktische Lernumgebung zur Vermittlung der objektorientierten Programmierung.
Die Bibliothek bietet die Möglichkeit eines didaktisch vereinfachten und intuitiven objektorientierten Zugangs zur dreidimensionalen Grafikprogrammierung mit OpenGL. Sie wurde speziell für den Einstieg in die Objektorientierung im Unterricht der gymnasialen Einführungsphase entwickelt und soll helfen, den Schülerinnen und Schülern in optisch ansprechender und motivierender Weise objektorientierte Zusammenhänge zu verdeutlichen.
Dreidimensionale Grafikprojekte
Autospiel
Mit Hilfe vorgegebener Klassen können Schülerinnen und Schüler im Anfangsunterricht dreidimensionale Animationen, Simulationen und Spiele entwickeln, ohne dass besondere Vorkenntnisse in der Mathematik oder in der Grafikprogrammierung erforderlich sind.
Die objektorientierte Modellierung und Programmierung kann schrittweise und begleitend mit den Grundlagen der Algorithmik, z. B. in Form von Kontrollstrukturen, eingeführt werden.
Neben den Klassen der GLOOP-Bibliothek steht der volle Umfang der Programmiersprache Java zur Verfügung.
Geometrische Körper als Grundelemente
geometrische Körper als Grundelemente
Jede Szene eines GLOOP-Programms wird aus geometrischen Körpern, wie z. B. Kugeln, Quadern, Zylindern und Kegeln, aufgebaut, die in einem dreidimensionalen, virtuellen Raum positioniert werden. GLOOP stellt fertige Klassen für diese und andere grafische Elemente zur Verfügung.
Mit einem für alle Körper einheitlichen Methodensatz können die Objekte im Raum z. B. verschoben, gedreht oder skaliert werden. Auf diese Weise können einfache Animation oder auch komplexe Simulationen erstellt werden.
Durch das Setzen von Färbungen und Texturen können die Oberflächen von Objekten gestaltet werden.
Objektorientierte Modellierung
Objektorientierte Modellierung
Der Schwerpunkt der Projektentwicklung kann ganz auf eine sinnvolle objektorientierte Modellierung gesetzt werden, da die grafische Darstellung des Projekts den Schülerinnen und Schülern weitgehend von GLOOP abgenommen wird.
Komplexere grafische Objekte können aus den grundlegenden geometrischen Körpern zusammengesetzt und mit Assoziations- und Vererbungsbeziehungen zueinander in Relation gesetzt werden.
Eingabe mit Tastatur und Maus
Eingabe mit Tastatur und Maus
Zur Steuerung von Projekten können die Tastatur und die Maus über zwei entsprechende Klassen abgefragt werden.
Schülerorientierte Programmierschnittstelle
Alle Klassen- und Methodenbezeichner der GLOOP-Bibliothek sind in deutscher Sprache gehalten und weitgehend selbsterklärend.
Es stehen Funktionalitäten für Einsteiger, aber auch für fortgeschrittene Schülerinnen und Schüler bereit, die über den eigentlichen Unterricht hinausgehen.
Schülerorientierte Programmierschnittstelle
Schülerorientierte Programmierschnittstelle
Alle Klassen- und Methodenbezeichner der GLOOP-Bibliothek sind in deutscher Sprache gehalten und weitgehend selbsterklärend.
Es stehen Funktionalitäten für Einsteiger, aber auch für fortgeschrittene Schülerinnen und Schüler bereit, die über den eigentlichen Unterricht hinausgehen.
Einbindung in BlueJ
Einbindung in BlueJ
Die Klassenbibliothek kann einfach in die didaktisch orientierte Entwicklungsumgebung BlueJ eingebunden werden.
Auch ein Arbeiten in anderen Umgebungen wie dem Java-Editor, Netbeans oder Eclipse ist möglich.
GLOOP ist plattformübergreifend und kann unter Windows, MaxOS und Linux verwendet werden.
Allgemeines
Die GLOOP-Umgebung simuliert einen dreidimensionalen Raum, der mit Hilfe eines Kameraobjekts vom Typ GLKamera in Echtzeit beobachtet werden kann. Der Raum ist zunächst leer und wird mittels eines dreidimensionalen, rechtshändischen Koordinatensystems strukturiert. Er erstreckt sich in die positive und in die negative Richtung aller Koordinatenachsen bis in die Unendlichkeit.
Aus vorgegebenen Klassen der GLOOP-Umgebung können Objekte erstellt werden, die automatisch in den dreidimensionalen Raum eingefügt werden. Dabei muss jeweils der Mittelpunkt und die Ausdehung des Objekts angegeben werden. Beispiele für solche Klassen sind: GLKugel, GLQuader, GLZylinder, GLWuerfel, GLKegel, GLKegelstumpf, GLTorus und GLPrismoid. Die Bezeichner der GLOOP-Klassen sind selbsterklärend und zeigen, um welche Sorte von Objekt es sich handelt. Sie beginnen mit dem Präfix GL, um später die Bezeichner der vorgefertigten GLOOP-Klassen besser von denen eigener Klassen unterscheiden zu können.
Damit die Objekte auch im Kamerabild zu sehen sind, muss die Szene noch durch ein Lichtobjekt vom Typ GLLicht ausgeleuchtet werden. Das einfachste sinnvolle GLOOP-Programm besteht also aus einem Kameraobjekt, einem Lichtobjekt und einem Objekt, das betrachtet wird.
Das Programm „Hello World!“
Um ein ganz einfaches GLOOP-Programm, das „Hello Word“-Programm, zu realisieren, wird die einzelne Klasse Kugeldemo erstellt und mit dem folgenden Quellcode implementiert:
| 1 import GLOOP.*; 2 class Kugeldemo { 3 GLKamera meineKamera; 4 GLLicht meinLicht; 5 GLKugel meineKugel; 6 7 Kugeldemo () { 8 meineKamera = new GLKamera(); 9 meinLicht = new GLLicht(); 10 meineKugel = new GLKugel (0,0,0, 50); 11 } 12 } |
Am Anfang der Klasse, d. h. in Zeile 1, wird die GLOOP-Bibliothek importiert. In der Deklaration wird jeweils ein Objekt vom Typ GLKamera, GLLicht und GLKugel angemeldet. Im Konstruktor werden die drei Objekte erstellt. Bei der Kugel wird die Stelle (0,0,0) als Mittelpunkt und der Wert 50 als Radius angegeben.
Das Erstellen einer Kamera führt dazu, dass ein Fenster aufspringt, in dem der virtuelle Raum in Echtzeit dargestellt wird. Die Standardposition der Kamera ist bei (0,0,500) mit Blick auf den Ursprung des Koordinatensystems. Die Lichtquelle leuchtet die Szene aus, so dass nun eine weiße Kugel zu sehen ist (vgl. Abbildung 2).
Abbildung 2: Kugel mit eingeblendeten Koordinatenachsen
Alle sichtbaren geometrischen Objekte, die im Raum platziert werden können, sind Spezialisierungen der Klasse GLObjekt und verfügen somit über den gleichen Methodensatz. Zum Beispiel kann jedes Objekt vom Typ GLObjekt mit einer Textur überzogen werden.
Die folgende Erweiterung macht aus der Kugel einen Globus, indem eine Textur der Erde ergänzt wird (vgl. Abbildung 3). Die in Zeile 11 angegebene Bilddatei muss dazu im aktuellen Projektordner liegen.
| 9 [...] 10 meineKugel = new GLKugel(0,0,0, 50); 11 meineKugel.setzeTextur("Erde.jpg“); 12 [...] |
Abbildung 3: Kugel mit Erdtextur
Animationen
Möchte man mehr als ein stehendes Bild zeigen, so muss eine Animationschleife ergänzt werden. Der folgende Quellcode stellt eine einfache, bewegte Simulation der sich drehenden Erde dar.
| 1 import GLOOP.*; 2 class Weltdemo { 3 GLKamera meineKamera; 4 GLLicht meinLicht; 5 GLKugel dieErde; 6 GLTastatur meineTastatur; 7 8 Weltdemo(){ 9 meineKamera = new GLKamera(); 10 meinLicht = new GLLicht(); 11 meineTastatur = new GLTastatur(); 12 13 dieErde = new GLKugel (0,0,0,150); 14 dieErde.setzeTextur ("Erde.jpg"); 15 dieErde.drehe(90,0,0); 16 this.starteAnimation(); 17 } 18 19 void starteAnimation(){ 20 while (!meineTastatur.esc()){ 21 dieErde.drehe(0,1,0); 22 Sys.warte(); 23 } 24 Sys.beenden(); 25 } 26 27 } |
In der obigen Klasse Weltdemo werden vier Objekte deklariert: eine Kamera, eine Lichtquelle, eine Kugel und ein Objekt zur Tastaturabfrage. Alle vier Objekte werden im Konstruktor der Klasse Weltdemo erstellt. Die Kugel wird zudem mit einer Erdtextur versehen und in Zeile 15 aus optischen Grün-den um 90 Grad gedreht.
In der Methode starteAnimation wird die Kugel von Zeile 20 bis Zeile 23 mit Hilfe der Animationsschleife bewegt. Diese Schleife läuft, solange nicht die Taste ESC gedrückt wurde. Bei jedem Durchlauf des Schleifenkörpers wird die Kugel mit Hilfe der Methode drehe um 1 Grad um die Y-Achse gedreht. Da die Kugel immer wieder um 1 Grad gedreht wird und die Kamera die Kugel kontinuierlich im aktuellen Zustand anzeigt, scheint die Kugel eine gleichmäßige Rotation durchzuführen (vgl. Abbildung 4). Der Aufruf der statischen Methode warte in Zeile 22 sorgt dafür, dass die Animation nicht zu schnell abläuft.
Abbildung 4: Animierte Erdkugel
Möchte man komplexere Simulationen realisieren, so wird man nicht mehr damit auskommen, einfachen geometrischen Objekten Aufträge zu erteilen. Vielmehr wir man dazu übergehen, mehrere Objekte zu neuen Klassen zusammenzufassen oder Objekte mittels Vererbung zu spezialisieren. Die in Abbildung 5 gezeigte Teilmodellierung einer Analoguhr gibt einen ersten Eindruck davon.
Abbildung 5: Analoguhr mit Teilmodellierung
Unterrichtsvorhaben
Hinweise zum unterrichtlichen Einsatz der GLOOP-Bibliothek sind im Lehrplannavigator SII Informatik zu finden. Dort werden im Beispiel für einen schulinternen Lehrplan die Unterrichtsvorhaben II – IV der Einführungsphase unter Verwendung der GLOOP-Bibliothek umgesetzt.
In den Materialien sind Projektbeschreibungen, Modellierungen und Quellcodes zu finden.
Einführung
In der objektorientierten Programmierung geht es darum, in einer Phase der Analyse und Modellierung einen realen Gegenstands- bzw. Problembereich mittels Abstraktion und Zusammenfassung in ein informatisches Modell zu überführen. Dieses Modell muss in seinem Komplexitätsgrad gegenüber der Wirklichkeit maßgeblich reduziert sein, ohne die Struktur des realen Gegenstandsbereiches bezogen auf die mit der Modellierung verbundene Aufgabe in unzulässiger Weise zu verzerren. Erst wenn eine solche Modellierung vorliegt, wird sie in Quellcode umgesetzt, welcher anschließend getestet werden kann.
Um sich mit grundlegenden Modellierungsaufgaben dieser Art befassen zu können, müssen zunächst einige Grundbegriffe geklärt werden. Dazu gehören in einem ersten Schritt die Begriffe Objekt, Klasse, Attribut und Methode. Da es sich hierbei um allgemeine Begriffe der Objektorientierung handelt, die in keiner speziellen Beziehung zu einer bestimmten Programmiersprache oder einem didaktischen Konzept stehen, sollten sie nicht nur programmiersprachenunabhängig, sondern auch komplett rechnerfrei behandelt werden.
Sequenzskizze
Zur Verdeutlichung dieser Grundbegriffe gibt es eine Reihe geeigneter Kontexte, wobei der Grundgedanke immer darin besteht, im Gegenstandsbereich eine Ansammlung verschiedener Objekte zu sehen. Ein Bahnhof besteht aus Gebäuden, Menschen und Zügen, ein Ampelkreuzung aus Fahrbahnen, Ampelanlagen und Fahrzeugen und ein Schule aus Lehrern, Schülern und Räumen. Dabei zeigt sich bereits an diesen einfachen Beispielen der Charakter der Modellbildung, der maßgeblich darin besteht, in sinnvoller Weise zu abstrahieren. Welche Abstraktion dabei als sinnvoll zu betrachten ist, hängt von der Aufgabe ab, zu deren Lösung die Modellierung erstellt wird.
Betrachten wir im Folgenden einen einfachen Gegenstandsbereich. Auf einer grünen Wiese steht ein einzelner Baum, in dessen Ästen sich eine Reihe von Vögeln niedergelassen haben. Nehmen wir weiter an, dass eine graphische Simulation dieser Szene erstellt werden soll. Unsere erste Aufgabe besteht nun darin, Objekte im Gegenstandsbereich zu identifizieren.
Der Baum besteht aus einem Stamm, Ästen, Blättern, und natürlich sind da die verschiedenen Vögel. Auf dem Boden sind Grashalme. All diese Objekte könnten sich in unserer Modellierung wiederfinden, insbesondere an den Vogelobjekten lassen sich die Grundprinzipien der Objektorientierung aber gut verdeutlichen. Dabei sollten wir uns an dieser Stelle nicht allein auf die Anforderungen dieser einfachen Aufgabe beschränken, sondern den Vogel auf eine solche Art und Weise modellieren, dass er auch in anderen, ähnlichen Simulationsprojekten wiederverwendet werden kann.



Abbildung 1: Verschiedene Vögel
Quellenangabe: Wikipedia Foundation Inc.; URL 1: http://de.wikipedia.org/wiki/Haussperling; URL 2: http://de.wikipedia.org/wiki/Blauhäher; URL 3: http://de.wikipedia.org/wiki/Saatkrähe; abgerufen: Dezember 2012.
Betrachtet man die in Abbildung 1 dargestellten Vögel, so fällt schnell auf, dass einzelne Vögel zwar sehr unterschiedlich sein können, prinzipiell aber immer vergleichbar sind. Es handelt sich durchgehend um flugfähige Tiere mit Federn, zwei Beinen, zwei Flügeln und einem Schnabel. In mancherlei Hinsicht unterscheiden sie sich aber auch. So ist ein Vogel womöglich etwas größer als ein anderer, hat eine andere Färbung des Gefieders oder ein anderes Geschlecht als sein Nachbar. Möchte man die drei Vögel in ihrer Individualität darstellen, so könnte das wie folgt aussehen.
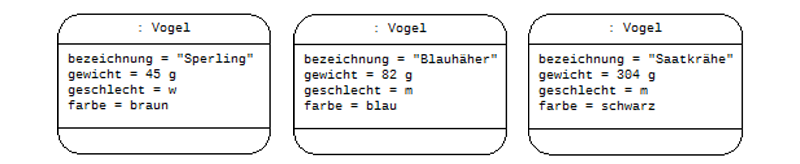
Abbildung 2: Objektdiagramm zu drei Vögeln
Alle Vögel sind im informatischen Sinne Objekte eines bestimmten Objekttyps bzw. einer bestimmten Objektklasse. Durch ihre Zugehörigkeit zu einem Objekttyp, in diesem Falle dem Typ Vogel, ist z.B. geklärt, dass es sich um Individuen mit Flügeln, Federn, Beinen und Schnabel handelt. Was jeden Vogel einzigartig macht, ist nicht mit dem Hinweis auf seine Typzugehörigkeit geklärt, sondern muss in jedem Vogelobjekt separat gespeichert werden. Vogelobjekte verfügen also über Attribute, die unterschiedliche Werte haben können. In diesem Fall sind das die Attribute art, gewicht, geschlecht und farbe.
Dabei werden nicht alle Unterschiede, die im Gegenstandsbereich vorhanden sind, im Modell auch abgebildet. Das informatische Modell stellt eine Vereinfachung dar, die abhängig von der informatischen Aufgabenstellung von Aspekten der Wirklichkeit abstrahiert. Oder anders ausgedrückt: möchte man z.B. eine graphische Simulation der Vögel erstellen, so ist es nicht notwendig, den Blutdruck einzelner Vögel in den Objekten zu verwalten. Er mag sich von Vogel zu Vogel zwar unterscheiden, ist für die Simulation aber ohne Relevanz.
Um die Modellierung zu vervollständigen, sollten die Objekte vom Typ Vogel noch um Methoden ergänzt werden, d.h. um Aufträge, die ein Vogelobjekt ausführen kann und um Anfragen, bei deren Aufruf das Vogelobjekt eine Auskunft erteilt. Das kann z.B. eine Auskunft über die Belegung eines Attributs sein.
Methoden und Attribute – nicht jedoch deren Belegung – sind für alle Objekte vom Typ Vogel gleich, so dass es Sinn macht, von der Klasse Vogel als eine Art Bauplan für Vogelobjekte zu sprechen.
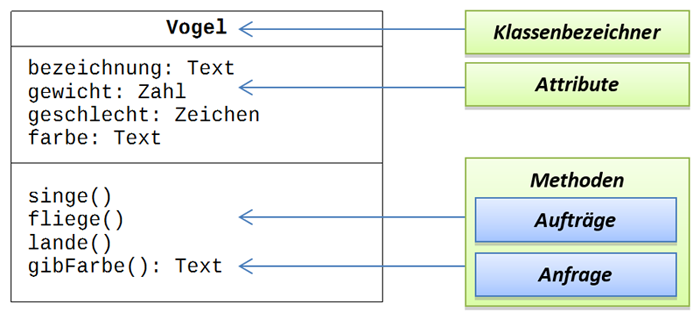
Abbildung 3: Klassendiagramm Vogel
Dieser Bauplan ist es, der letztlich programmiert wird. Aus ihm werden dann beliebig viele Objekte vom Typ Vogel erstellt.
Während die Modellierung einer Vogelklasse auf diese Weise sinnvoll erscheint, kann es andere Kontexte geben, bei der eine Klasse sich maßgeblich dadurch auszeichnet, dass sie aus anderen Klassen zusammengesetzt ist. Diese Komposition ist die einfachste Form der Klassenbeziehung und sollte bereits am Anfang thematisiert werden. So könnte man sich z.B. eine Klasse Schwarm vorstellen, wobei ein Schwarm sich aus Objekten vom Typ Vogel zusammensetzt. Der Schwarm selbst könnte dann wieder über Attribute und Methoden verfügen.
Spätestens an dieser Stelle sollte ein weiterer Aspekt der Objektorientierung angesprochen werden, der darin besteht, dass der Prozess der objektorientierten Bearbeitung eines Gegenstandsbereichs nicht sofort mit der Modellierung von Objekten und Klassen beginnen sollte. Der erste Schritt ist stets eine Analyse des Problembereichs. Mit anderen Worten: ein gewisses Grundverständnis der Funktionsweise eines Schwarms und des Verhaltens sowie des Aufbaus eines Vogels muss vorhanden sein, um eine angemessene Modellierung durchzuführen. Während das in vielen Beispielkontexten, die in der Schule bearbeitet werden, noch recht einfach ist, nimmt diese Analysephase bei größeren Projekten immer mehr Raum ein.
Von einem eigentlichen Modellierungsprozess im informatischen Sinne sind wir aber noch immer entfernt. Dazu müsste die Modellbildung zielgerichteter sein. Diese Zielsetzung bestimmt, von welchen Aspekten des Gegenstandsbereiches abstrahiert werden kann, ohne die Funktionsfähigkeit des zu erstellenden Softwareproduktes in Frage zu stellen. Bisher wurde nur gesagt, dass eine graphische Simulation erstellt werden soll, nicht aber, was sie alles leisten soll.
Schulische Projekte im Bereich der objektorientierten Modellierung und Programmierung sollten daher dem aus der Fachwissenschaft bekannten Wasserfallmodell der Softwareentwicklung in didaktisch reduzierter Form folgen.
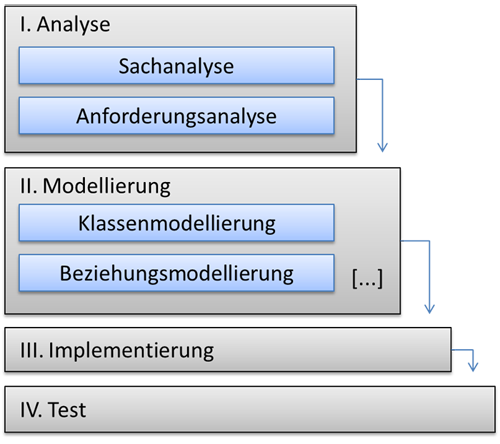
Abbildung 4: vereinfachtes Wasserfallmodell
- Analyse
Gegenstandsbereich und Aufgabenstellung werden von den Schülerinnen und Schülern erfasst bzw. erarbeitet. Dazu gehört auch ein Anforderungsprofil für das zu erstellende Produkt. - Modellierung
Klassen und deren Beziehungen werden unter Berücksichtigung der Analysephase entworfen. Je nach Anforderungen des Projektes kann das ein einfaches Beziehungsdiagramm oder auch eine komplexere Modellierung bestehend aus Entwurfsdiagramm und Implementationsdiagramm sein. - Implementierung
Die Modellierung wird unter Verwendung einer geeigneten didaktischen Umgebung in Quellcode umgesetzt. Dabei kann in vielen Fällen mit einem vom Kursleiter erstellten bzw. überarbeiteten Prototyp gearbeitet werden, der von den Kursteilnehmern ergänzt werden soll. Auf diese Weise werden zeitaufwändige Implementationsarbeiten ohne didaktischen Wert vermieden. - Test
Der implementierte Quellcode wird hinsichtlich der in der Analysephase erarbeiteten Anforderungen getestet. Bei einfacheren Projekten geschieht dies nur implizit. Bei komplexeren Projekten können hier auch Qualitätskriterien wie z.B. das Laufzeitverhalten des Programms berücksichtigt werden.
Sequenzielle Programmierung
Nachdem die grundlegende Idee der Objektorientierung verdeutlicht wurde, soll ein erstes objektorientiertes Programm am Rechner erstellt werden. Dabei wird zunächst rein sequenziell gearbeitet, d.h. es werden keine Kontrollstrukturen wie Schleifen oder Verzeigungen verwendet. Die Schülerinnen und Schüler können sich also ganz auf grundlegende Aspekte der Java-Syntax, der Entwicklungsumgebung BlueJ und des GLOOP-Pakets konzentrieren.
Materialien:
- Entwicklungsumgebung BlueJ (www.bluej.org)
- GLOOP – Bibliothek (Bereich Installation)
- Einführungsphase UV II.3 (Link)
Sequenzskizze
Um die Schülerinnen und Schüler in die Lage zu versetzen, ihr erstes Programm zu erstellen, muss zunächst eine allgemeine Einführung in die didaktische Umgebung GLOOP und die Entwicklungsumgebung BlueJ gegeben werden. Das GLOOP-System kann als ein Paket bereits fertig erstellter Klassen betrachtet werden, die eine dreidimensionale Visualisierung von geometrischen Objekten im Raum ermöglichen. Aus Klassen können Objekte erstellt werden, sie verfügen über Attribute und stellen bestimmte Dienste zur Verfügung.
Des Weiteren kommt ein sinnvolles Programm nur dann zustande, wenn mehrere Objekte unterschiedlichen Typs in konstruktiver Weise zusammenwirken. Wird ein GLOOP-Programm gestartet, so simuliert der Rechner einen endlosen dreidimensionalen Raum, der durch ein rechtshändisches Koordinatensystem strukturiert wird. Wird ein Objekt vom Typ GLKamera erzeugt, so öffnet sich ein Fenster, das den simulierten Raum wie eine Videokamera in Echtzeit aufnimmt. Ein GLOOP-Programm benötigt also mindestens ein Kameraobjekt, um die programmierte Szene sichtbar zu machen.
Der Inhalt der so zu beobachtenden Szene wird aus sogenannten GLObjekten zusammengesetzt, die alle über einen identischen Methodensatz verfügen und sich in der Regel lediglich im Konstruktor unterscheiden.
Folgende GLObjekte stehen als geometrische Grundbausteine für GLOOP-Programme zur Verfügung: GLKugel, GLQuader, GLZylinder, GLWuerfel, GLKegel, GLKegelstumpf, GLTorus und GLPrismoid (siehe Abbildung 1).
Wird eines dieser Objekte instanziiert, muss im Konstruktor seine Position und typabhängig seine Ausdehnung angegeben werden. Anschließend können Position, Drehung, Größe und Oberfläche des Objektes mit Hilfe von Aufträgen verändert werden. Für eine vollständige Beschreibung des Funktionsumfangs steht die Dokumentation des GLOOP-Systems zur Verfügung.
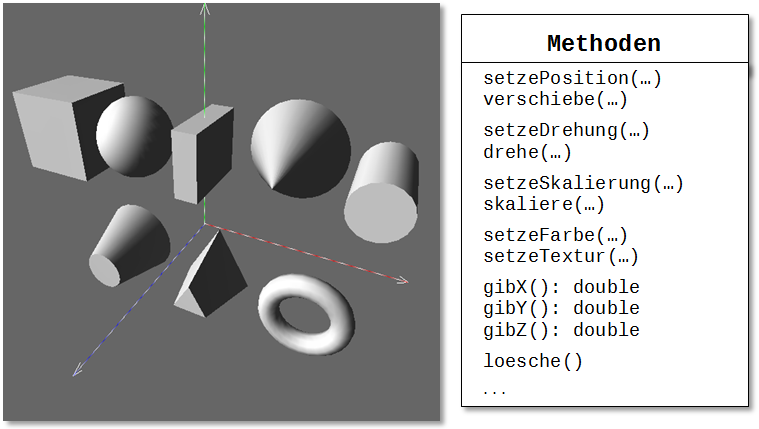
Abbildung 1: Überblick über die wichtigsten Objekte und Methoden eines GLOOP-Objekts
Um das Erstellen und Manipulieren von Objekten zu erproben, kann der Direkteingabemodus von BlueJ verwendet werden. Auf diese Weise können Objekte erstellt werden, ohne dass ein vollständiger Programmcode implementiert wird. Darüber hinaus sind Zustandsänderungen von Objekten unmittelbar nach einem Methodenaufruf zu beobachten.
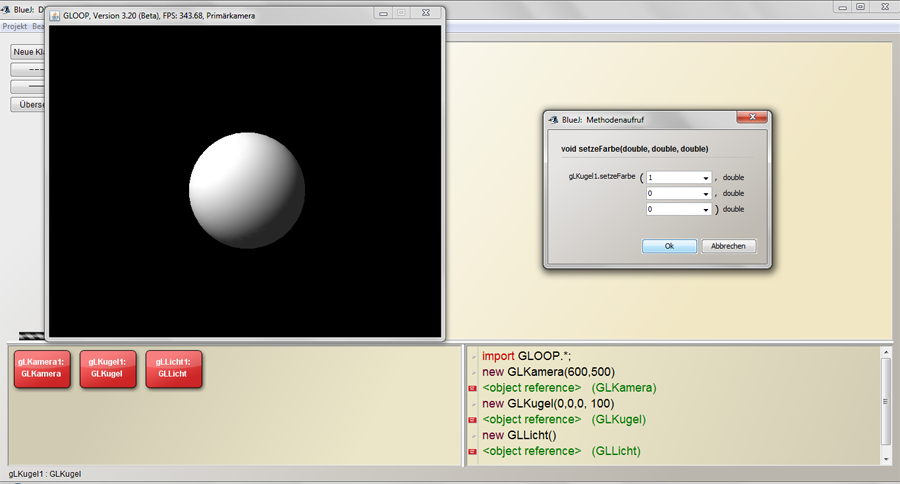
Abbildung 2: Eine GLKugel im Direktmodus von BlueJ
Abbildung 2 zeigt, wie im Direktmodus von BlueJ eine Kugel erzeugt wird. Zunächst wird im Direkteingabefenster das GLOOP-Paket mit import GLOOP.*; importiert. Anschließend wird eine Kamera mit den Bildabmessungen 600 mal 500 Bildpunkte und im Koordinatenursprung eine Kugel mit dem Radius 100 erzeugt. Damit die Kugel auch zu sehen ist, wird zum Schluss noch eine Lichtquelle erzeugt.
Über einen Rechtsklick auf die roten Objektkästchen am linken unteren Bildschirmrand können die Schülerinnen und Schüler nun Dienste des jeweiligen Objektes aufrufen. Abbildung 2 zeigt, wie der Dienst setzeFarbe des Objektes glKugel1 aufgerufen wurde.
Mit Hilfe dieser Direkteingabe können Schülerinnen und Schüler das Erstellen von Objekten und Aufrufen von Methoden erproben und direkt die entsprechende Reaktion des Programms beobachten.
Natürlich stößt diese Methode schnell an ihre Grenzen, da bei jedem Neustart die komplette Befehlssequenz neu eingegeben werden muss. Die Lösung für dieses Problem besteht darin, eine Klasse zu erstellen, die nicht nur ein Objekt in der Szene darstellt, sondern vielmehr einen Bauplan für die gesamte Szene beinhaltet. Der Quellcode für die in Abbildung 2 im Direktmodus erstelle Miniszene wird den Kursteilnehmern als Prototyp zur Verfügung gestellt und kann als Ausgangspunkt für eigene Szenen verwendet werden.
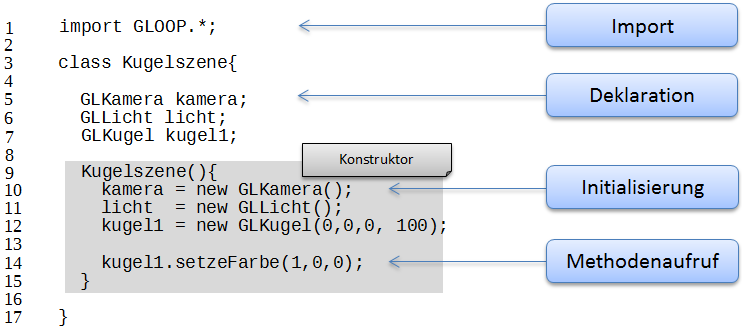
Am Beispiel dieses Prototypen lassen sich Begrifflichkeiten wie Import, Deklaration, Konstruktor, Initialisierung und Methodenaufruf mit Punktnotation klären. Um sie einzuüben, kann die Szene von den Schülerinnen und Schülern verändert und erweitert werden.
Eine Möglichkeit, die sich hier anbietet, ist das Projekt Skulpturengarten. Darin wird eine Szene erstellt, die über einen Boden und einen Himmel verfügt und auf dem Boden, der durch eine entsprechende Textur wie eine Wiese aussieht, verschiedene GLObjekte zeigt. Da sie mit einer Marmortextur versehen sind, wirken sie wie Skulpturen in einem Garten oder Park.

Abbildung 3: Ein Skulpturengarten mit sechs kreisförmig angeordneten Objekten
Ein interessanter Aspekt dieses Beispiels besteht darin, dass bereits in der Modellierungsphase überlegt werden kann, wie die einzelnen GLObjekte am besten in einer kreisförmigen Anordnung zu platzieren sind. Die Koordinaten der Objekte so zu berechnen, dass sie einen Kreis bilden, ist zwar ohne größeren Aufwand möglich, das Problem lässt sich aber deutlich einfacher lösen, wenn die Rotationsmethoden der GLObjekte verwendet werden.
Bei dieser Strategie werden alle Skulpturen an derselben Stelle erstellt und anschließend um einen bestimmten Punkt im Raum gedreht, der dann zum Mittelpunkt des Skulpturenrings wird. Die Objekte selbst werden auf ihren Sockeln um den eigenen Mittelpunkt rotiert, so dass sich ein ansprechenderes Erscheinungsbild ergibt.
Wie bei allen sequenziellen GLOOP-Programmen ist auch diese Szene statisch. Da es keine Schleifen gibt, die für kontinuierliche Zustandsänderungen der Objekte sorgen könnten, entsteht ein unbewegliches Bild. Wird aber eine Kamera vom Typ GLSchwenkkamera erstellt, können die Schülerinnen und Schüler diese Kamera mit Hilfe der Maus um den Koordinatenursprung drehen, so dass sie ihre Szene von allen Seiten betrachten können.
Vertiefung
Sequenzielle GLOOP-Programme bestehen im Grunde nur aus dem Erstellen und Manipulieren von Objekten, die anschließend so zusammenwirken, dass sie dreidimensionales Bild ergeben. Eine Vertiefung besteht also darin, weitere interessante und womöglich auch anspruchsvollere Bilder zu erstellen. Der Fantasie sind an dieser Stelle keine Grenzen gesetzt.
Zu bevorzugen sind aber solche Projekte, bei denen der Übungseffekt zeitökonomisch zu erzielen ist, d.h. nicht Dutzende von Objekten in mühsamer Kleinarbeit zu platzieren sind. Sinnvoll ist es Aufgaben zu wählen, bei denen bereits in der Planungsphase eine Herausforderung zu sehen ist. Ein Beispiel dieser Art ist die Modellierung und Umsetzung der Olympischen Ringe.

Abbildung 4: Olympische Ringe
Noch bevor an die Umsetzung am Rechner zu denken ist, müssen einige Frage geklärt werden. Nicht allen Schülerinnen und Schülern wird klar sein, welche Farben die Ringe eigentlich haben. Da die Farbe eine GLObjektes im RGB-Modus gemischt wird, stellt sich die Frage nach eben dieser Mischung der Farben. Und letztlich muss geklärt werden, wie die Ringe eigentlich im Raum zu drehen sind, damit sie korrekt ineinanderfassen.
Kontrollstrukturen
Nachdem das Erstellen und Manipulieren von Objekten ohne die Verwendung von Kontrollstrukturen behandelt wurde, sollen diese nun zusammen mit anderen Inhalten am Beispiel eines einfachen Spiels eingeführt werden.
Materialien:
- Einführungsphase UV III.1 (Link)
Sequenzskizze
Das Projekt Ballwurfspiel besteht darin, ein einfaches Spiel zu entwickeln. Ziel des Spiels ist es, mit einem Ball eine zufällig platzierte Zielscheibe zu treffen. Der Ball kann mit der Tastatur nach links, rechts, oben und unten bewegt und so in die richtige Position gebracht werden. Auf Tastendruck fliegt er nach vorne weg, bis er auf Höhe der Zielscheibe ist. Ein Treffer bzw. Fehlwurf sollte mit einer Meldung angezeigt werden.
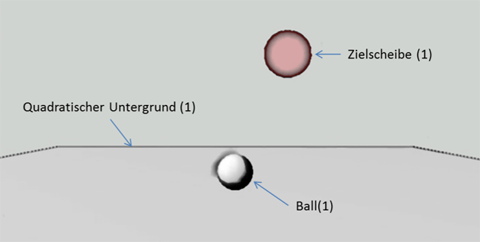
Abbildung 1: Planungsskizze zum Projekt Ballwurfspiel
Mit Hilfe der Planungsskizze (siehe Abbildung 1) können die Schülerinnen und Schüler sehr schnell sehen, welche GLObjekte nötig sind, um das Spiel zu realisieren. Neu ist an diesem Projekt, dass die Szene nun dynamisch auf eine Eingabe reagieren soll. Es soll eine Tastenabfrage realisiert werden und der Ball soll sich bewegen. Um das Grundprinzip der Eingabe und Animation zu verdeutlichen, wird der folgende Prototyp vorgegeben und kann von den Schülerinnen und Schülern analysiert werden.
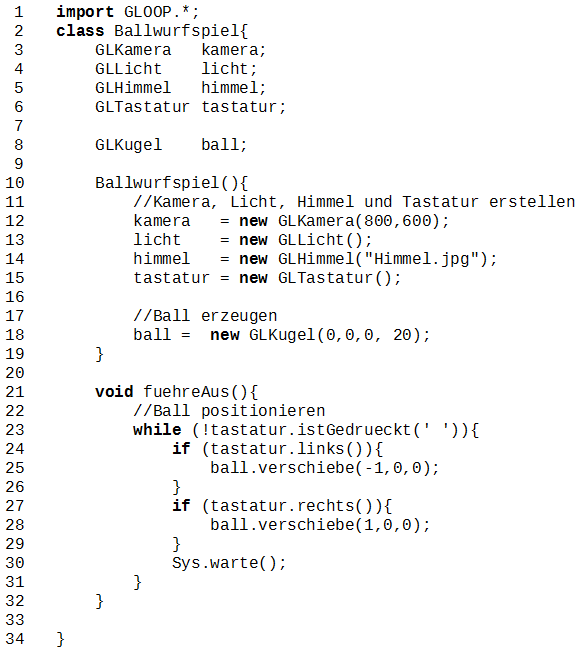
Code Ballwurfspiel
Im Konstruktor des Prototypen werden Kamera, Licht, Himmel und eine Kugel erzeugt. Da auf eine Tastatureingabe reagiert werden soll, wird des Weiteren ein Objekt vom Typ GLTastatur erstellt, mit dem diese Eingabe abgefragt werden kann.
Die Methode fuehreAus() muss vom Nutzer in der BlueJ-Umgebung nach Start des Programm per Hand aufgerufen werden und beinhaltet eine Schleife, welche solange läuft, wie die Tastatur nicht meldet, dass die Taste SPACE gedrückt wurde. Innerhalb dieser Schleife wird mit zwei Verzweigungen nach dem Druck der Taste Pfeil-Rechts bzw. Pfeil-Links gefragt. Ist eine dieser Tasten gedrückt, so wird die Kugel verschoben. Die Methode realisiert also eine einfache Tastatursteuerung für die Kugel.
Der Prototyp demonstriert den einfachen Gebrauch einer Schleife, einer Verzweigung und einer Anfrage an ein Objekt. Durch schrittweise Erweiterung dieses Prototyps kann nun das oben beschriebene Spiel realisiert werden. Da die Abläufe im Spiel aber komplizierter sind als im obigen Prototyp, ist es zu empfehlen, diese zunächst in Form von Struktogrammen zu realisieren. Im Prinzip besteht unser Spiel nämlich aus drei Schritten bzw. Phasen.
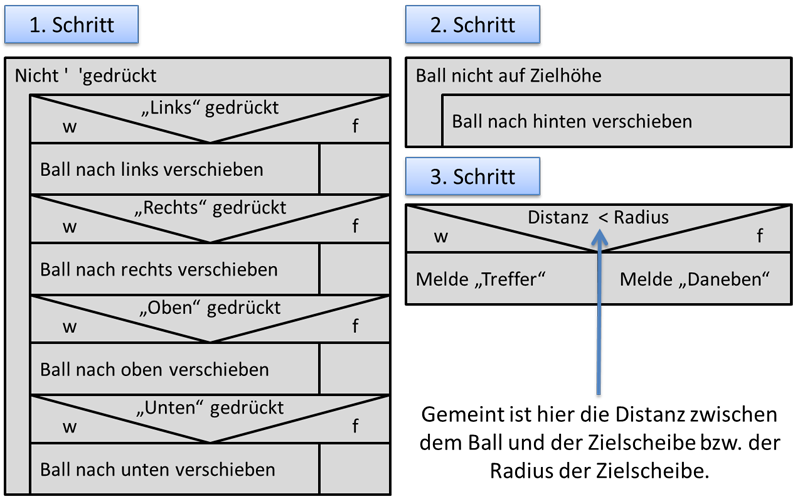
Abbildung 2: Struktogramme zum Projekt Ballwurfspiel
In Schritt 1 wird eine Schleife ausgeführt, in der man den Ball in einer Ebene verschieben kann. Wird die Taste SPACE gedrückt, endet die Schleife und es wird zu Schritt 2 übergegangen. Hier wird durch eine zweite Schleife die gleichmäßige Flugbewegung des Balles nach hinten weg realisiert, welche endet, wenn er auf Höhe der Zielscheibe angekommen ist. Anschließend wird in Schritt 3 entschieden, ob die Zielscheibe getroffen ist, und die entsprechende Meldung ausgegeben.
Eine Realisierung dieser Schritte könnte im Quellcode wie folgt aussehen:

Quellcode Ball positionieren
Während Schritt 1 eine direkte Erweiterung des Prototypen darstellt, kommen in Schritt 2 und Schritt 3 jeweils neue Aspekte hinzu. In Schritt 2 wird eine Anfrage an ein GLObjekt gestellt, die als Rückgabe einen Zahlenwert liefert, und in Schritt 3 wird in Abhängigkeit von einem Variablenwert eine Ausgabe gesetzt. Der Variablenwert wird zuvor mittels des Satzes des Pythagoras berechnet. Hierbei handelt es sich um eine einfache Distanzberechnung zwischen Zielscheibe und Wurfball, um zu entscheiden, ob die Zielscheibe getroffen wurde. Je nach Erfolg des Wurfes wird eine entsprechende Meldung mit Hilfe eines Objektes vom Typ GLTafel ausgegeben.
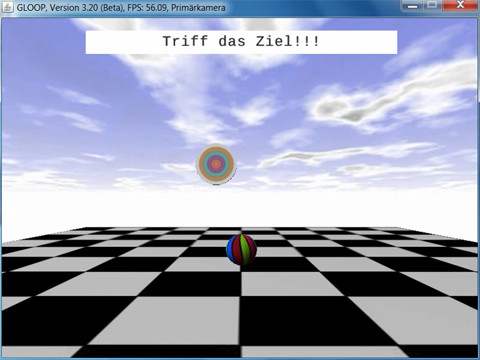
Abbildung 3: Texturierte Version des Projekts Ballwurfspiel
Während dieses Beispiel gut geeignet ist, Schleifen, Verzeigungen und auch Variablen einzuführen, müssen diese Konzepte im Weiteren eingeübt werden. Neben der Möglichkeit, weitere Animationen nach obigem Muster zu erstellen, können Schleifen dazu verwendet werden, um größere Mengen von Objekten zu erstellen und zu manipulieren. Da es in einem solchen Fall aufwändig wäre, zu jedem Objekt eine einzeln deklarierte Referenz zu erstellen, bietet sich die Verwendung von Feldern an, so dass mit Hilfe eines Index’ auf sehr viele Objekte zugegriffen werden kann.
Ein Beispiel könnte in diesem Kontext die Simulation eines Hubschrauberlandeplatzes sein, der mit mehreren Signallampen in Form von kleinen Kugeln ausgestattet ist. Diese Kugeln sind kreisförmig um den Landeplatz angeordnet und stellen Lauflichter da, d.h. sie ändern nacheinander ihre Farbe.
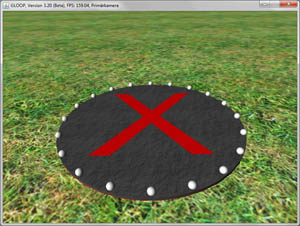
Abbildung 4: Landeplatz mit Signallampen
Abbildung 4 zeigt eine mögliche Realisierung dieses Hubschrauberlandeplatzes. Wie und in welcher Reihenfolge die Kugellampen ihre Farbe ändern, kann ganz unterschiedlich realisiert werden. Der folgende Quellcode starteLauflichter() stellt eine sehr einfache Lösung dar. Alle Lampen werden nacheinander angeschaltet und anschließend nacheinander wieder ausgeschaltet. Dieser Vorgang wiederholt sich, bis der Benutzer mit der Taste ESC abbricht.
Die Lampen werden hier in einem Feld mit dem Bezeichner lampe verwaltet.

Code starte Lauflichter
Eine weitere Möglichkeit besteht darin, die Lampen gleichzeitig blinken zu lassen. Hierzu müssen nur die Aufrufe der Methode warte() an anderen Stellen erfolgen.
Beispiele, die auf Feldern basieren, sind insbesondere zur Thematisierung der FOR-Schleife geeignet. Möchte man diese weiter vertiefen, kann man sie auch schachteln, z.B. zur Simulation eines Schachbretts.
Vertiefung
Das Schachbrett wird hier nicht mit Hilfe einer Textur, sondern durch einzelne Quader realisiert. Sie werden in zwei geschachtelten Schleifen erzeugt und in einem Feld verwaltet.

Abbildung 5: Schachbrett aus einzelnen Quadern
Folgender Quellcode stellt eine Möglichkeit da, die Felder zu erzeugen.

Code Schachbrett
Eigene Klassen
In der folgenden Sequenz soll das Erstellen eigener Klassen in den Blickpunkt gerückt werden. Dazu gehört nicht nur die Implementation eigener Klassen in Java, sondern auch die Modellierung einer Problemstellung mit Hilfe eigener Klassen. Das Prinzip der Vererbung wird später behandelt und hier zunächst ausgespart.
Materialien:
- Einführungsphase UV III.3 (Link)
Sequenzskizze
Im Folgenden soll ein Einstieg in die Verwendung eigener Klassen mit Hilfe des Projektes „Kerzen“ beschrieben werden. Das Projekt besteht darin, eine Simulation von drei brennenden Kerzen auf einem Holzbrett zu erstellen.
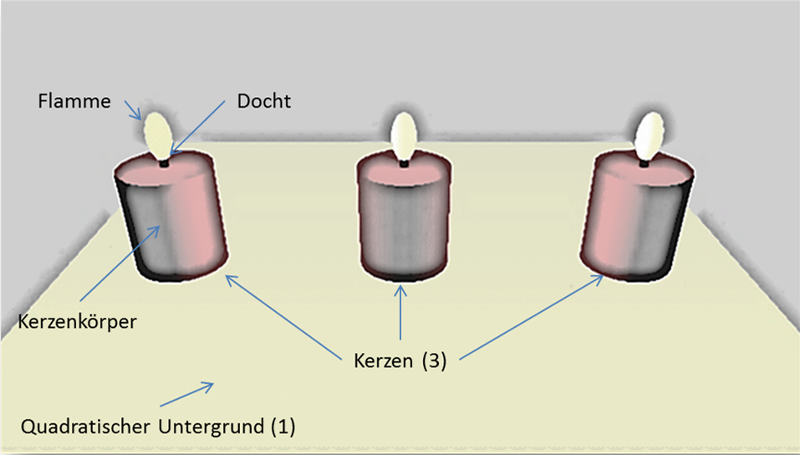
Abbildung 1: Planungsskizze zum Projekt Kerzen
Der Körper einer jeden Kerze besteht aus einem Objekt vom Typ GLZylinder, ebenso wie der jeweilige Docht einer Kerze. Die Flamme selbst ist ein Objekt vom Typ GLLicht, welches sich, sofern sichtbar geschaltet, als kleine Kugel zeigt. Diese kann mittels der Methode skaliere() zur endgültigen Flammenform verzerrt werden. Der Untergrund der Kerzen besteht aus einem mit Holztextur überzogenen Objekt vom Typ GLQuader.
Jede Kerze soll in der Simulation an- und ausgemacht werden können. Sofern sie gerade an ist, brennt sie ab, bis sie nur noch einen kurzen Stumpf darstellt und von selbst erlischt. Sie kann dann nicht mehr angezündet werden. Wie schnell eine Kerze abbrennt, ist abhängig von ihrer Dicke. Je dicker eine Kerze ist, umso langsamer brennt sie ab.
Auch bei diesem Projekt wird den Schülerinnen und Schülern wieder ein Prototyp vorgegeben, den es zunächst zu analysieren gilt. Im Gegensatz zu bekannten Programmen besteht dieser jedoch bereits aus drei rudimentären Klassen.

Code Kerzenszene
Wird der Prototyp in der Entwicklungsumgebung BlueJ geladen, präsentiert er sich mit diesen drei Klassen, die in Form von drei Klassenkästen angezeigt werden. Da den Schülerinnen und Schülern Programme mit mehr als einer Klasse nicht vertraut sind, stellt sich zunächst die Frage, wie der Prototyp eigentlich zu starten ist. Erst die Instanziierung aller drei Klassen per Hand führt zum gewünschten Ergebnis, und eine Kerze wird angezeigt.
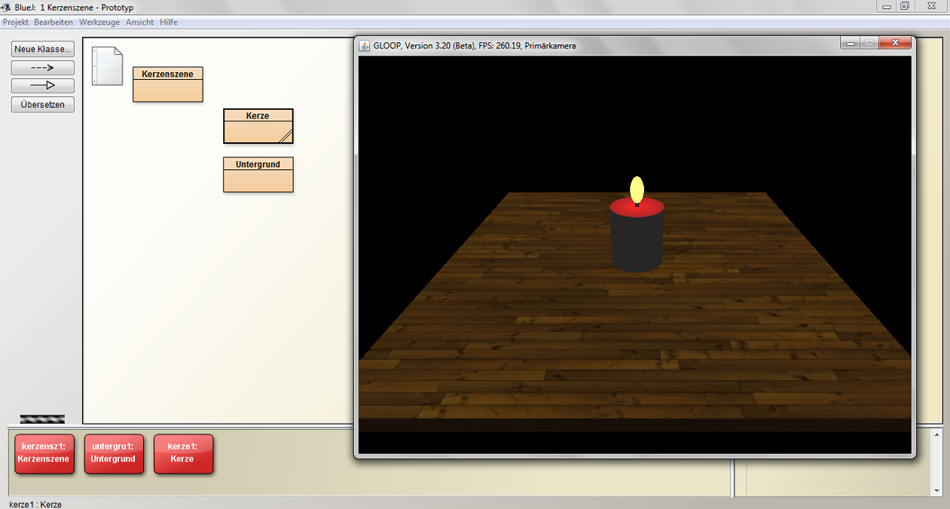
Abbildung 2: Laufender Prototyp zum Projekt Kerzen
Auf diese Weise demonstriert der Prototyp, dass alle in einem BlueJ-Projekt enthaltenen Klassen in einem Programmkontext zu sehen sind und gemeinsam eine lauffähige Simulation ergeben können. Welche Objekte erstellt wurden, ist am linken unteren Ende des BlueJ-Fensters zu sehen.
Der Prototyp liefert so zwar ein lauffähiges Ergebnis, ist von unseren Anforderungen aber noch weit entfernt. Es wird nur eine Kerze gezeigt, diese lässt sich nicht ausmachen und brennt auch nicht ab.
Mehr als eine Kerze zu erstellen, sollte jedoch kein Problem sein. Intuitiv könnte man auf den Gedanken kommen, dass einfach nur ein weiteres Objekt vom Typ Kerze erzeugt werden muss. Führt der Kursteilnehmer oder die Teilnehmerin diesen Plan aus, kommt es zu einem interessanten Ergebnis. Es erscheint keine weitere Kerze im Bild, das Bild wird aber heller. Bei genauerer Überlegung wird schnell klar, woran das liegt. Es erscheint nämlich doch eine weitere Kerze im Bild, welche die Helligkeit der Szene durch ihre Flamme erhöht. Sie befindet sich aber an exakt der gleichen Stelle wie die erste Kerze und ist daher optisch nicht als separates Objekt wahrzunehmen. Mit diesem Phänomen als Motivation lassen sich nun Zustandsvariablen, Parameter und Methoden einführen. Eine ausführlichere Modellierung des Projektes Kerzen könnte dann wie folgt aussehen.
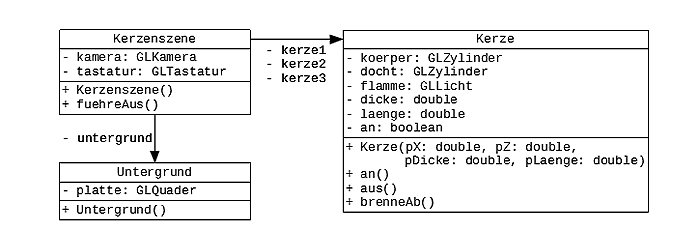
Abbildung 3: Modellierung des Projekts Kerzen
Im Konstruktor der Klasse Kerzenszene werden Untergrund und Kerzen erstellt. Die Methode fuehreAus() beinhaltet eine Animationsschleife, in der mit Hilfe einer Tastaturabfrage die Methoden an() bzw. aus() der einzelnen Kerzen aufgerufen werden können. Des Weiteren wird für jede Kerze die Methode brenneAb() aufgerufen.
Die Kerzen selbst bestehen aus einer Komposition von zwei Zylindern und einer Lichtquelle. Die beiden Zylinder stellen den Kerzenkörper und den Docht dar, während die Lichtquelle für die Flamme der Kerze steht.
Die Methoden an() bzw. aus() lassen die Lichtquelle erscheinen bzw. verschwinden, wohingegen die Methode brenneAb() abhängig von der Dicke der Kerze und der Information, ob die Kerze gerade an ist, ihre Länge mittels Skalierung und Verschiebung reduziert. Sie lässt, wie der Name schon sagt, die Kerze abbrennen, bis sie eine Minimallänge unterschreitet und dann ausgemacht wird.
Um das zu realisieren, muss die Kerze ihren eigenen Zustand in einer Reihe von Variablen nachhalten. Dicke, Länge und die Information, ob sie gerade an ist, werden in entsprechenden Attributen gespeichert und von den Methoden verwendet. Die Position der Kerze wird zwar im Konstruktor übergeben, so dass nicht alle Kerzen an derselben Stelle zu sehen sind, sie wird aber nicht in neuen Zustandsvariablen gespeichert. Die Position der Kerze ist nur dann von Bedeutung, wenn die GLObjekte erstellt werden, aus denen die Kerze besteht. Zu einem späteren Zeitpunkt muss diese Position nicht mehr abgefragt werden, so dass keine Notwendigkeit besteht, sie in Zustandsvariablen nachzuhalten.

Abbildung 4: Laufende Kerzenszene mit drei Kerzen
Darüber hinaus lässt sich an diesem Beispiel das Geheimnisprinzip der objektorientierten Programmierung verdeutlichen. Könnte man aus der Klasse Kerzenszene auf das Attribut an zugreifen, so könnte man die Kerze zum Abbrennen bringen, obwohl gar keine Flamme zu sehen ist und auf diese Art die Funktionsweise eines Kerzenobjekts kompromittieren. Die Attribute der Klasse Kerze sollten also geschützt werden, indem ein Zugriff von außerhalb der Klasse verweigert wird. Ist dieser Mechanismus einmal eingeführt, sollte er im weiteren Verlauf des Moduls bei allen Attributen und Methoden zum Einsatz gebracht werden, indem diese als privat oder öffentlich deklariert werden.
Der folgende Quellcode stellt die Methode brenneAb() der Klasse Kerze dar:

Code Abbrennvorgang
Die Methode brenneAb() zeigt sehr zutreffend den Charakter eines Dienstes im Sinne der objektorientierten Programmierung. Zwar stellt die Methode den Auftrag dar abzubrennen, die Kerze zeigt aber ein - wenn auch rudimentäres - selbstgesteuertes Verhalten und brennt nur dann ab, wenn die Kerze auch an ist. Objekte, die innerhalb klar definierter Grenzen autonom Aufträge interpretieren, sind typisch für die Objektorientierte Programmierung.
Eine geringfügige mathematische Schwierigkeit stellt die Längenreduktion der Kerze dar. Die lokale Variable g errechnet die Längenreduktion in Abhängigkeit von der Kerzendicke.
Das Attribut laenge wird mit laenge = laenge – g entsprechend angepasst. Die optische Verkürzung der Kerze wird über den Dienst skaliere() der Klasse GLObjekt durchgeführt. Zur Verkürzung der Länge des Zylinders koerper um den Wert g muss also ein entsprechender Skalierungsfaktor errechnet werden. Dieser Skalierungsfaktor ergibt sich durch den Term 1.0 – (g / laenge). Diese Umrechnung kann vermieden werden, indem von Anfang an mit einem Skalierungsfaktor gearbeitet wird. In dem Fall wird die Kerze aber nur schwer so zu realisieren sein, dass sie gleichmäßig abbrennt.
Vertiefung
Um die am Kerzenbeispiel eingeführten Inhalte und insbesondere die Modellierung mit Hilfe eigener Klassen einzuüben, bietet sich das Projekt Analoguhr an. Bei diesem Vorhaben soll eine Szene erstellt werden, in der drei Uhren mit unterschiedlichen Zeitzonen angezeigt werden.
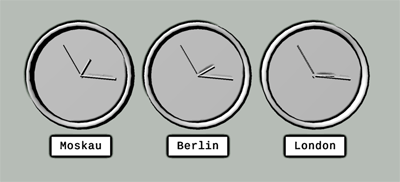
Abbildung 3: Planungsskizze zum Projekt Analoguhren
Um dieses Projekt zu realisieren, sind verschiedene Modellierungen möglich, so dass Schülerinnen und Schüler einen Eindruck vom kreativen Aspekt der informatischen Modellierung bekommen können. Verschiedene Modellierungen können erstellt, verglichen und bewertet werden, wobei nicht nur implementationstechnische, sondern auch logische Bewertungskriterien Berücksichtigung finden sollten.
Eine mögliche Modellierung dieses Projektes soll im Folgenden dargestellt werden:

Abbildung 4: Implementationsdiagramm zum Projekt Analoguhren
Die Klasse Uhrenszene erstellt drei Uhren, stellt ihre Zeit und verfügt über eine Animationsschleife, die einmal pro Sekunde die Methode weiter() aller drei Uhren aufruft.
Beim Erstellen einer Uhr muss deren Position in der XY-Ebene und der Name des Ortes angegeben werden, der als Schriftzug unter der Uhr erscheinen soll.
Die Uhr erstellt daraufhin ihr Ziffernblatt und ihre Anzeigetafel mit dem entsprechenden Schriftzug. Beide Elemente sind statisch und werden sich im weiteren Verlauf der Simulation daher nicht verändern. Des Weiteren werden drei Objekte vom Typ Zeiger erstellt: der Sekunden-, Minuten- und Stundenzeiger. Sie erhalten unterschiedliche Längen und Dicken, so dass sie voneinander zu unterscheiden sind. Darüber hinaus wird ihnen eine Geschwindigkeit mitgegeben. Entsprechende Werte werden in Zustandsvariablen gespeichert.
Die Methode stelleZeit() der Klasse Uhr und die Methode stelleDich() der Klasse Zeiger sind zum direkten Setzen der Uhrzeit beim Programmstart gedacht.
Bekommt die Uhr nun den Auftrag weiter(), so ruft sie die gleichlautenden Methoden ihrer drei Zeiger auf. Diese werden sich dann entsprechend ihrer in Attributen gespeicherten Geschwindigkeiten drehen. Der Sekundenzeiger wird 60 Aufrufe dieser Methode benötigen, um einmal über das Ziffernblatt zu wandern, der Minutenzeiger 3600 (60*60) und der Stundenzeiger 43200 (12*60*60).
Zu bedenken ist bei dieser Modellierung, dass sowohl die Uhr als auch die Zeiger über keine Attribute zum Speichern der aktuellen Zeit verfügen. Die Uhrzeit ergibt sich lediglich aus der Stellung der Zeiger auf dem Ziffernblatt. Man kann argumentieren, dass dies aus der Perspektive der Modellierung unglücklich ist, da jede Uhr im Zustand einer bestimmten Zeitanzeige ist und somit auch entsprechende Zustandsvariablen haben sollte. Andererseits ergibt sich auch bei einer realen Analoguhr die Uhrzeit allein aus der Stellung der Zeiger, ohne dass sie an einer anderen Stelle gespeichert wird.
Ist die Modellierung erstellt, erweist sich die Implementierung in den meisten Fällen als recht einfach. Der folgende Quellcode stellt die Klasse Zeiger dar. Sie ist nach obiger Modellierung die komplexeste Klasse des Projekts:

Code class zeiger
Assoziationen
Während zuvor bereits eigene Klassen eingeführt und mit einfachen Beziehungen versehen wurden, soll im Folgenden der Datenfluss zwischen mehreren Objekten genauer behandelt werden. Bisher haben Objekte nur Zugriff auf andere Objekte gehabt, wenn sie diese selbst erstellt haben. Für komplexere Probleme reicht das nicht mehr aus. Soll ein Objekt Zugriff auf eines haben, das nicht selbst erstellt wurde, so muss im Konstruktor oder in einer Methode eine entsprechende Referenz als Parameter übergeben werden. Das bedeutet, dass auf dasselbe Objekt von verschiedenen Stellen über verschiedene Bezeichner zugegriffen werden kann. Das setzt bei den Schülerinnen und Schülern ein tieferes Verständnis von Referenz voraus, das im folgenden Modul erarbeitet werden soll.
Materialien:
- Einführungsphase UV IV.1 (Link)
Sequenzszene
Der Einstieg in dieses Modul erfolgt mit Hilfe einer klassischen Spielidee. Es soll ein Spiel programmiert werden, in dem am unteren Bildschirmrand ein kleines Ufo zu sehen ist und vom Spieler mit den Pfeiltasten nach links und rechts bewegt werden kann.
Von oben kommen nun Asteroiden herangeflogen, denen es auszuweichen gilt. Wird das Ufo von einem Asteroid getroffen, so ist das Spiel zu Ende.
Zunächst soll das Spiel mit lediglich drei Asteroiden realisiert werden. Des Weiteren befinden sich alle Objekte in der XY-Ebene, d.h. es wird zweidimensional modelliert.
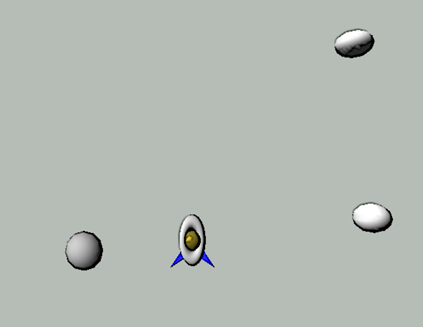
Abbildung 1: Planungsskizze zum Projekt Ufospiel
Eine Analyse dieses Problem führt schnell zu dem Ergebnis, dass ein Ufo aus mehreren GLObjekten besteht, die synchron verschoben werden müssen, wenn das Ufo ausweicht. Eine solche Komposition ist bereits bekannt.
Das Problem liegt hier im Detail, wenn man sich fragt, wie die Kollision zwischen einem Ufo und einem Asteroiden realisiert werden soll. Ein mögliches Vorgehen besteht darin, dieses Problem zunächst auszuklammern und lediglich die Steuerung des Ufos und die Bewegung der Asteroiden zu realisieren. Eine entsprechende Modellierung ohne Kollision sieht dann wie folgt aus:
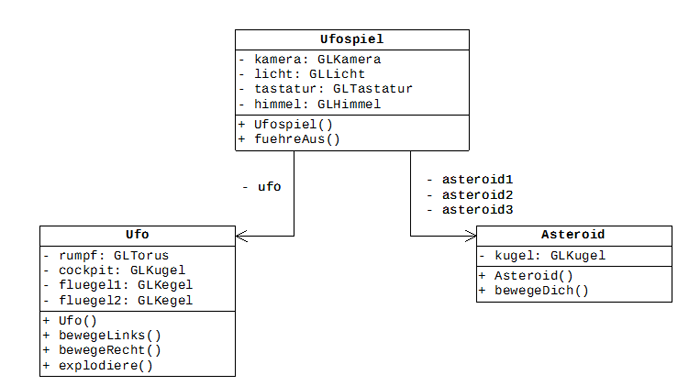
Abbildung 2: Modellierung eines einfachen Prototypen ohne Kollision
Ein entsprechendes Programm kann von den Schülerinnen und Schülern entweder selbst entwickelt werden oder in Teilen als Prototyp vorgegeben und analysiert werden.
Eine gute Idee ist es, das Programm so zu erweitern, dass ein Asteroid, der am unteren Ende aus dem Kamerabild gewandert ist, an eine neue Position jenseits des oberen Randes des Erfassungsbereichs der Kamera gesetzt wird, so dass er erneut auf das Ufo zufliegen kann. Auf diese Weise kann mit nur drei Objekten ein stetiger Strom von Hindernissen simuliert werden.
Das Zurücksetzen des Asteroiden kann in eine entsprechende private Methode ausgelagert werden.
Abgesehen davon muss die Kollision noch realisiert werden. Hierbei sollte jeder Asteroid Zugriff auf das Ufo erhalten, so dass er eine Kollision abprüfen kann und ggf. die Methode explodiere() des Ufos aufrufen kann. Dazu wird eine Referenz auf das Ufo im Konstruktor des Asteroiden übergeben und von ihm gespeichert. Die erweiterte Modellierung sieht dann wie folgt aus:
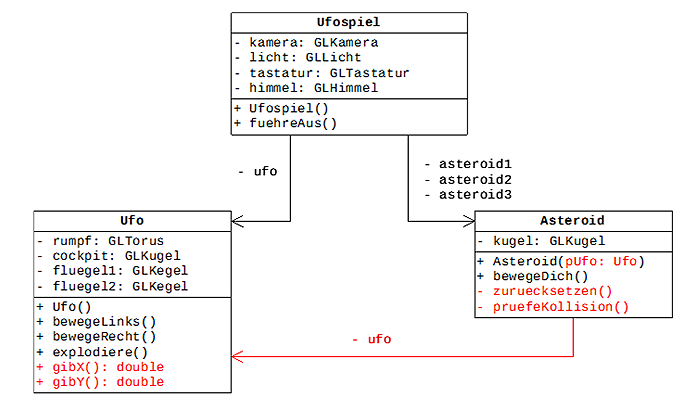
Abbildung 3: Modellierung eines einfachen Prototypen mit Kollision
Die Methoden zuruecksetzen() und getroffen() sind privaten Methoden der Klasse Asteroid und werden in bewegeDich() von Asteroid aufgerufen. Die Methode getroffen() testet auf eine Kollision mit dem Ufo und liefert den Wert true, wenn eine vorliegt. Die Methode bewegeDich() von Asteroid wird das Ufo dann zur Explosion bringen.
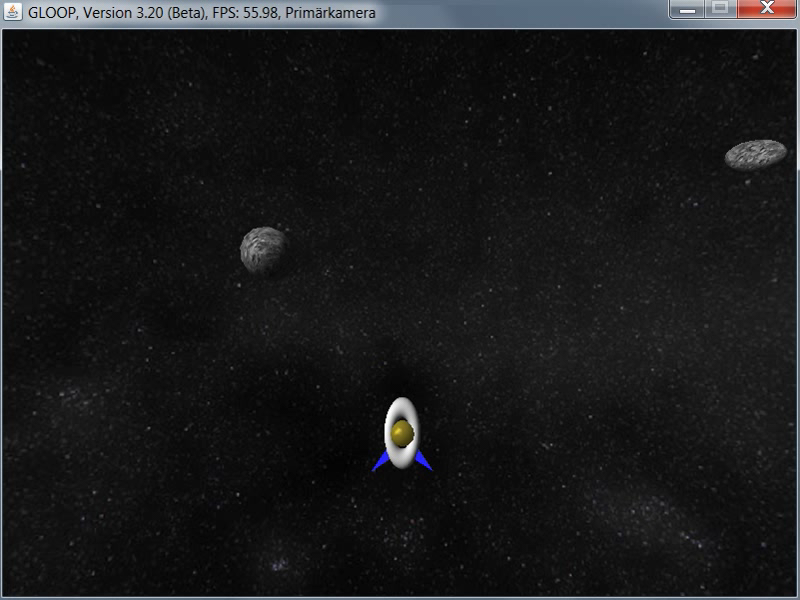
Abbildung 4: Das Ufospiel in zwei Dimensionen
Um zu entscheiden, ob eine Kollision vorliegt, berechnet der Asteroid mittels des Satzes des Pythagoras die Distanz zwischen ihm und dem Ufo. Dazu muss er die Position des Ufos mit Hilfe der Methoden gibX() und gibY() anfragen können. Ist die Distanz unter einem gewissen Schwellenwert, so wird eine Kollision angenommen.
Zu bedenken ist an dieser Stelle, dass auf das Objekt vom Typ Ufo nun von zwei verschiedenen Stellen aus zugegriffen werden kann. Dazu kommen zwei Referenzen zum Einsatz, die sogar den gleichen Bezeichner tragen können, da sie in unterschiedlichen Klassen sind.

Quellcode
Ist das Ufospiel auf diese Weise fertiggestellt, könnte ein erster Erweiterungsschritt darin bestehen, es auf die dritte Dimension zu erweitern. Die Kamera wird dazu um 90 Grad gekippt und die Bewegung des Ufos um die Methoden bewegeOben() und bewegeUnten() erweitert. Die Positionierung der Asteroiden wird ebenfalls um eine Dimension erweitert, ebenso wie die Berechnung der Distanz zwischen Asteroiden und Ufo auf drei Dimensionen umgestellt werden muss.
Da nun deutlich mehr Platz zum Ausweichen vorhanden ist, sollte die Anzahl der Asteroiden unter Verwendung eines Feldes erhöht werden. Das Ergebnis könnte eine Simulation wie in Abbildung 5 sein.
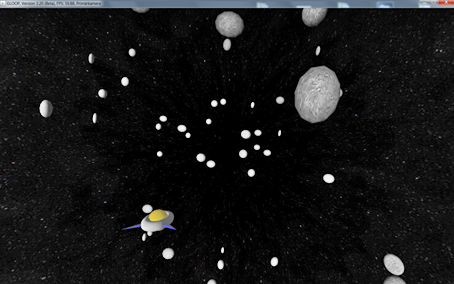
Abbildung 5: Das Ufospiel in drei Dimensionen
Natürlich ist es auch möglich, eine Geschwindigkeitsänderung des Spiels einzubauen, mehrere Fehlschläge zu erlauben, bevor das Spiel zu Ende ist oder einen Laser zu ergänzen, mit dessen Hilfe Asteroiden aus der Bahn geschossen werden können.
Vertiefung
Um das Prinzip der mehrfachen Referenzierung von Objekten zu vertiefen, stehen mehrere Projektideen zur Verfügung, die auf einer ähnlichen Modellierung wie das Ufospiel beruhen.
Eine Alternative stellt das Projekt Kugelfangen dar. Dabei bewegen sich auf einem quadratischen Spielfeld drei Kugeln. Erreichen sie den Rand des Spielfelds, ändern sie die Richtung, so dass sie das Spielfeld nicht verlassen. Der Spieler steuert eine kleine Fangbox über das Spielfeld und soll eine Kollision mit den Kugeln herbeiführen und sie auf diese Weise „fangen“. Ist eine Kugel gefangen, so verschwindet sie. Sind alle Kugeln gefangen, ist das Spiel zu Ende.
Die Fangbox wird vom Spieler so gesteuert, dass er jeweils die neue Bewegungsrichtung der Box mit der Tastatur angeben kann. Die Box läuft dann von allein immer weiter in die entsprechende Richtung. Droht sie das Spielfeld zu verlassen, ändert sie ebenfalls automatisch die Richtung.
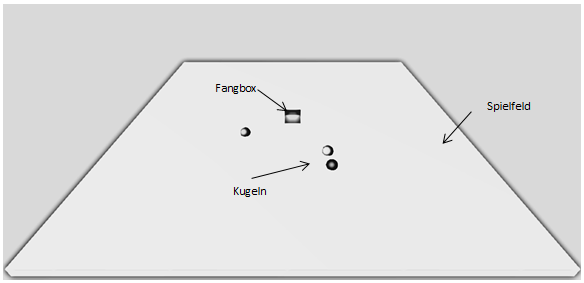
Abbildung 6: Planungsskizze zum Projekt Kugelfangen
Eine Modellierung zu diesem Projekt sollte die Klassen Kugelfangen, Kugel, Box und Spielfeld umfassen. Modellierungen im Kontext der Bibliothek Stifte und Mäuse oder in Greenfoot verzichten in der Regel auf die Klasse Spielfeld, da sie den Bildschirm als Spielfeld interpretieren. Da die GLOOP-Bibliothek aber keinen Bildschirm kennt, muss hier eine gesonderte Klasse entwickelt werden. Eine mögliche Modellierung könnte wie folgt aussehen:
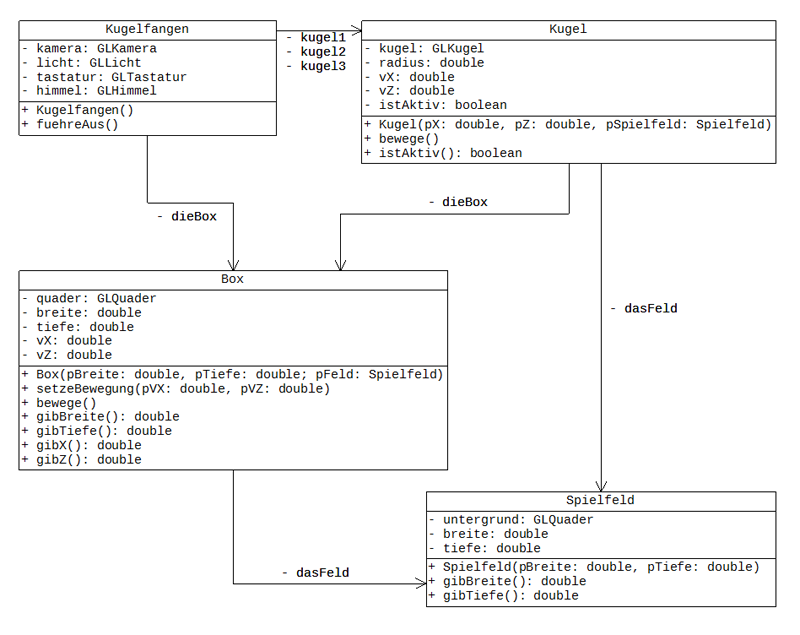
Abbildung 7: Modellierung des Projekts Kugelfangen
Durch das Erstellen eines Objektes der Klasse Kugelfangen wird das Spiel gestartet. Es erstellt alle anderen Objekte und ruft in einer Animationsschleife für die Box und die drei Kugel die Methode bewege() auf. Abhängig von einer Tastatureingabe wird die Methode setzeBewegung() der Box aufgerufen. Ihr wird mit Hilfe von zwei Parametern die neue Bewegungsrichtung der Box übergeben, wobei pVX die Bewegungskomponente in X-Richtung ist und pVZ die Bewegungskomponente in Z-Richtung. Das Spiel ist also in der XZ-Ebene modelliert. Sowohl die Box als auch die Kugel überprüfen bei ihrer Bewegung, ob sie am Rand des Spielfeldes angekommen sind. Dazu können sie auf das Spielfeld zugreifen und seine Breite bzw. Tiefe abfragen. Die Kugeln überprüfen darüber hinaus, ob eine Kollision mit der Box vorliegt und setzen sich ggf. inaktiv und unsichtbar.
Das Spiel beendet sich, wenn alle Kugeln inaktiv sind.
Der folgende Quellcode stellt die Methode bewege der Kugel dar:
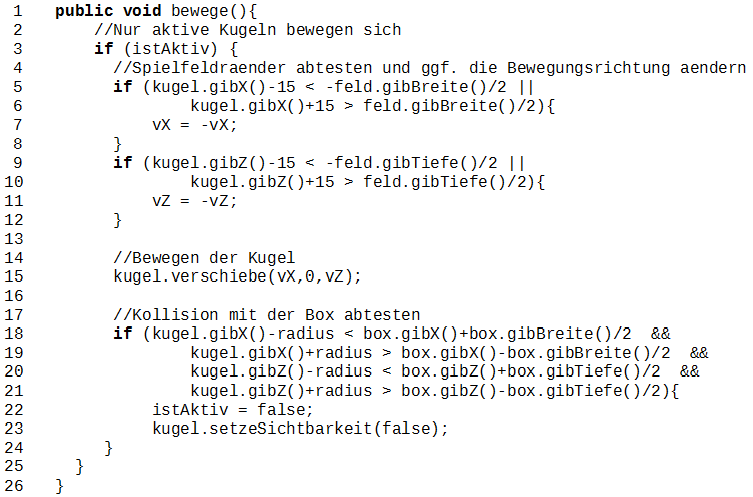
Quellcode Methode der Bewegung der Kugeln
Das fertige Ergebnis kann dann wie in Abbildung 8 gezeigt aussehen.
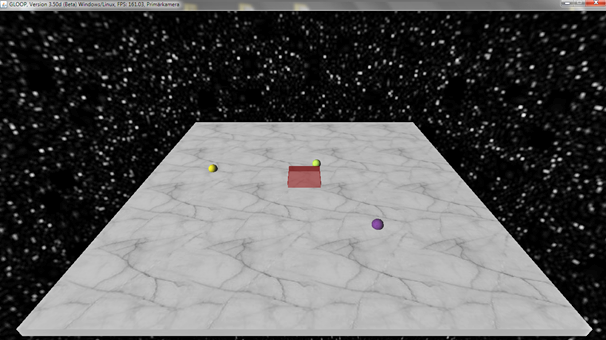
Abbildung 8: Modelllösung des Projekts Kugelfangen
Natürlich können mit Hilfe eines Feldes problemlos auch mehr als drei Kugeln realisiert werden. Auch die Spielregeln können noch angepasst werden. So könnte z.B. die Box beim Verlassen des Spielfelds nicht automatisch die Richtung ändern, sondern über den Rand stürzen und so das Spiel beenden. Des Weiteren könnte ein Punktezähler eingebaut werden. Das Spiel könnte dann beim Erreichen einer bestimmten Punktzahl zu Ende sein. Vor dem Erreichen dieser Punktzahl tauchen immer neue Kugeln auf.
Neben diesen beiden Projekten gibt es eine große Anzahl weiterer Möglichkeiten, um Objektbeziehungen dieser Art einzuüben. So könnte z.B. ein Auto durch einen Wald fahren oder ein Billardtisch mit tickenden Kugeln bestückt werden.


Abbildung 9: Autofahren und Billard als weitere Vertiefungsmöglichkeiten
Vererbung
In dieser Sequenz werden die wichtigsten Spielarten der Vererbung anhand dreier Projekte vorgestellt. Den Anfang macht das Projekt Schneemannsimulation, in dem die Vererbung als Spezialisierung im Sinne einer einfachen Erweiterung einer Oberklasse vorgestellt wird.
Darauf folgt das Projekt Flummisimulation, welches das Verständnis von Vererbung um den Aspekt der späten Bindung erweitert. Es werden also Dienste der Oberklasse überschrieben.
Zum Abschluss wird am Beispiel Tannenbaumsimulation das Prinzip der abstrakten Klasse eingeführt.
Materialien:
- Einführungsphase UV IV.1 (Link)
Sequenzszene
Der Einstieg in dieses Modul erfolgt mit Hilfe der Simulation eines einzelnen Schneemanns. Dieser kann entweder als Übung von den Schülerinnen und Schülern selbst erstellt oder aber als Prototyp vorgegeben werden.
Das Projekt Schneemannsimulation
Von der Modellierung her ist entscheidend, dass der Schneemann als eigene Klasse realisiert wird, so dass ggf. auch mehrere Schneemänner in einer Szene erstellt werden können. Der Schneemann selbst besteht aus drei Kugeln, zwei Augen und einer Nase und hat ggf. Knöpfe auf der Brust. Die Abbildung 1 zeigt einen einfachen Schneemann ohne Knöpfe.
Abbildung 1: Ein einfacher Schneemann als Oberklasse
Da der Schneemann über einen Konstruktor verfügt, der ihn an unterschiedliche Stellen in der Szene positionieren kann, ist es ohne Probleme möglich, auch mehrere Schneemänner zu realisieren.
Sinn dieses Projektes ist es nun, eine solche Gruppe von Schneemännern zu erstellen, die jedoch nicht alle ganz identisch aussehen. Vielmehr soll eine internationale Schneemanngruppe erstellt werden, wobei sich die Schneemänner aus unterschiedlichen Erdeilen durch ihre Kopfbedeckung unterscheiden.

Abbildung 2: Internationale Schneemänner durch Vererbung
Die Realisierung dieser Schneemänner kann nun mit Hilfe der Vererbung geschehen, indem im Konstruktor der Unterklasse die jeweilige Kopfbedeckung ergänzt wird. Es wird die folgende Modellierung vorausgesetzt.
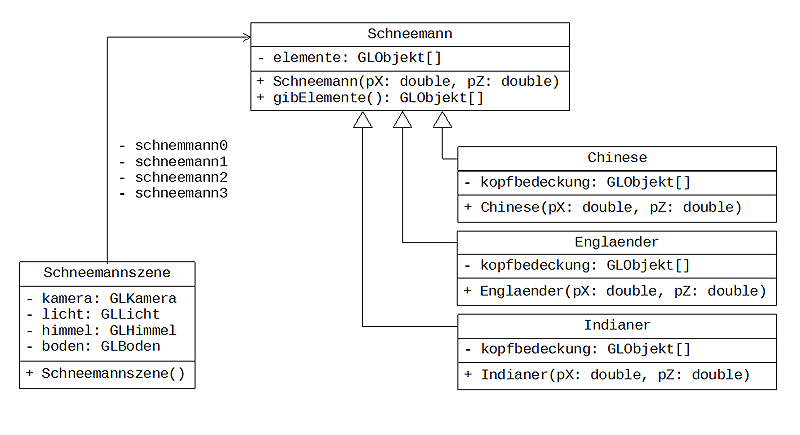
Abbildung 3: Modellierung der Schneemänner
Möchte man diese Modellierung mit den Schülerinnen und Schülern zusammen erarbeiten, so bietet es sich an, diese Aufgabe zunächst ohne den Mechanismus der Vererbung zu planen. Man kommt dann zu dem Ergebnis, dass verschiedene Schneemanntypen verschiedene Klassen mit großen Redundanzen sind oder aber, dass eine Kopfbedeckung eine eigene Klasse sein sollte. Eine andere Realisierung stellt die oben gegebene Modellierung dar. Jeder Schneemann verfügt über ein Feld von Typ GLObjekt, in dem seine Elemente gespeichert werden. Jede Unterklasse von Schneemann hat ein weiteres Feld, das seine Kopfbedeckung beinhaltet. Da das Feld elemente der Oberklasse Schneemann privat ist und zumindest für den Chinesenschneemann ein Zugriff auf die Augen möglich sein muss, hat die Klasse Schneemann eine Methode gibElemente, die das Feld zurückliefert und es somit manipulierbar macht. Der Chinesenschneemann kann so seine Augen zu Schlitzen skalieren.
Zu berücksichtigen ist, dass an dieser Stelle die Vererbung gleich in zweifacher Hinsicht verwendet wird. Zum einen erben die speziellen Schneemänner von ihrer Oberklasse und zum anderen wird die Klasse GLObjekt als Oberklasse für alle in der Szene zu sehenden Elemente verwendet. Sowohl Kugeln als auch Zylinder, Kegel oder Toren können also in einem gemeinsamen Feld verwaltet werden.
Hat man die Vererbung auf diese Weise thematisiert, kann ein komplexeres Projekt in Angriff genommen werden, bei dem es notwendig wird, eine Methode zu überschreiben. Das Prinzip des late-bindings lässt sich gut am Projekt Flummisimulation verdeutlichen.
Das Projekt Flummisimulation
Das Projekt beginnt mit einem einfachen Prototyp. Dieser Prototyp lässt einen einzelnen Ball zwischen zwei Hindernissen hin- und herticken. Er folgt der in Abbildung 4 gezeigten Modellierung.
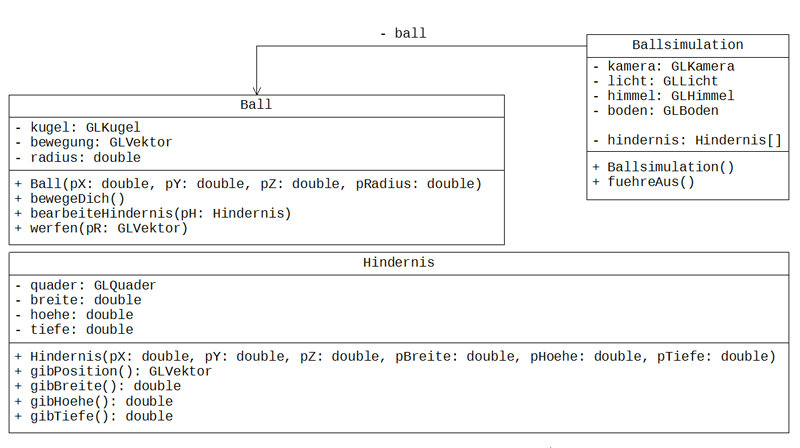
Abbildung 4: Modellierung der Flummisimulation (Prototyp)
Dieser Prototyp kann nun erweitert werden, indem spezielle Varianten des Balls ergänzt werden. Dazu wird jeweils eine Unterklasse von Ball erstellt. Da die unterschiedlichen Ballvarianten sich nicht nur im Aussehen unterscheiden sollen, muss auch die Bewegung des Balls variiert werden. Um den jeweiligen Ball zu bewegen, wird die Methode bewegeDich in einer Animationsschleife der Klasse Ballsimulation aufgerufen. Je nachdem wie diese Methode realisiert ist, können unterschiedliche Bewegungsvarianten realisiert werden. Folgende Modellierung setzt verschiedene Ballvarianten um.
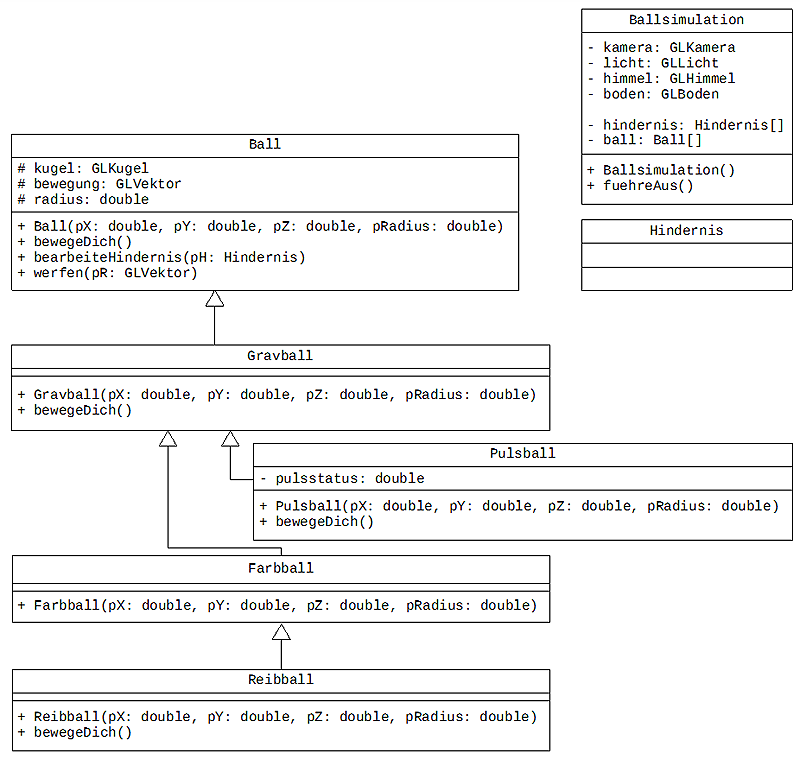
Abbildung 5: Modellierung der Flummisimulation (Modelllösung)
Die Klasse Gravball steht für einen Ball, der durch die Gravitation angezogen wird und vom Boden der Szene abtickt. Ein Farbball hat eine Zufallsfarbe und ein Reibball wird mit der Zeit langsamer, so dass er liegen bleibt. Der Pulsball verändert während der Animation seine Größe, er pulsiert. Alle Attribute der Klasse Ball werden als protected deklariert, damit ein Zugriff aus den Unterklassen möglich ist.
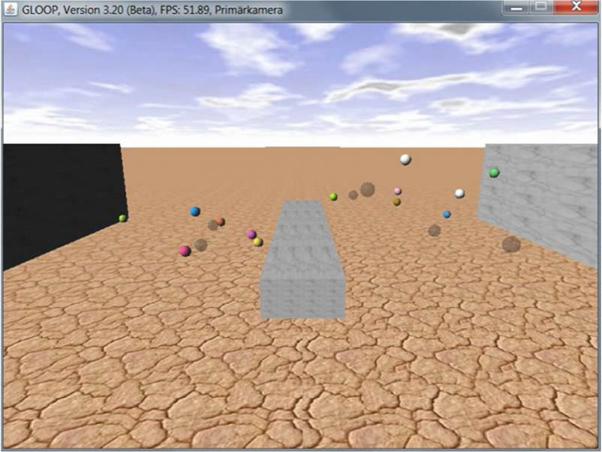
Abbildung 5: Flummisimulation mit verschiedenen Bällen
Alle Bälle können mit Hilfe eines Feldes vom Typ Ball in der Klasse Ballsimulation verwaltet werde. Da die Methode bewegeDich zum Teil überschrieben wird, sind sie nicht nur in ihrem Aussehen, sondern auch in ihrem Verhalten unterschiedlich.
Die hier aufgeführten Unterklassen von Ball sind exemplarisch zu verstehen. Natürlich sind noch weitere Varianten möglich. Darüber hinaus könnten unterschiedliche Arten von Hindernissen erstellt werden, die sich bei einer Kollision mit einem Ball unterschiedlich verhalten.
Vertiefung
Um tiefer in das Prinzip der Vererbung einzusteigen, wenden wir uns einer Simulation eines Weihnachtsbaums zu. Dabei soll ein Tannenbaum mit verschiedenen Arten von Schmuckstücken versehen werden, die durch unterschiedliche geometrische Objekte dargestellt werden. Es gibt Kugeln, Päckchen in der Form von Würfeln und Zuckerringe in Form von Toren.
Wir beginnen mit einem Prototyp, der bereits mit Kugeln geschmückt werden kann. Die Klasse Kugel hat dabei zwei Methoden.
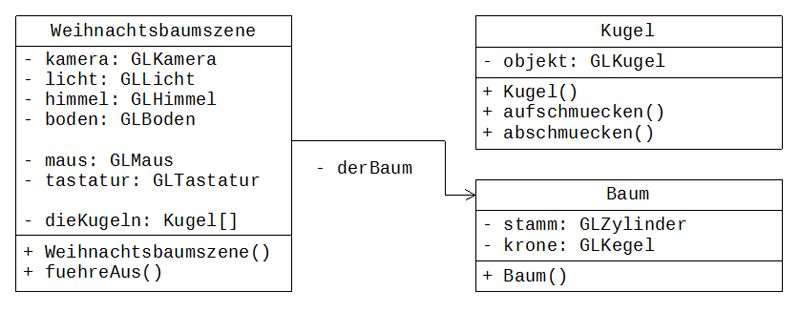
Abbildung 6: Modellierung I der Weihnachtsbaumsimulation (Prototyp)
Die Methode abschmuecken setzt die Y-Koordinate der Kugel auf 0, so dass die Kugel nicht mehr am Baum ist, sondern auf dem Boden liegt. Die Kugel wird also abgeschmückt. Die Methode aufschmuecken positioniert die Kugel wieder an einer zufälligen Stelle auf den Baum. Sie wird also aufgeschmückt.
Der Prototyp soll auf dem Hintergrund des Prinzips der Vererbung so erweitert werden, dass die anderen Arten der Schmuckstücke ebenfalls eingebaut werden.
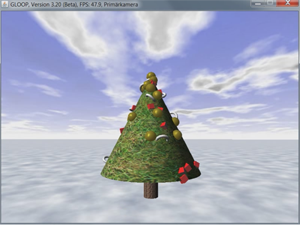
Abbildung 7: Weihnachtsbaumsimulation mit verschiedenen Schmuckstücken
Da alle Schmuckstücke über die Funktion des Auf- und Abschmückens verfügen sollen, liegt es nahe, dass diese Methoden in einer gemeinsamen Oberklasse realisiert werden.
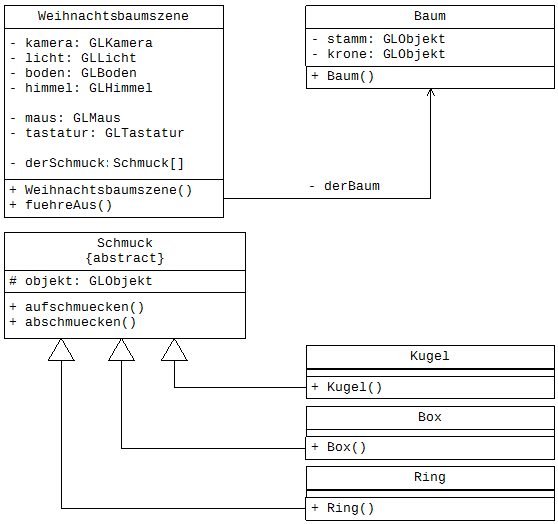
Abbildung 8: Modellierung der Weihnachtsbaumsimulation mit abstrakter Klasse
Abbildung 8 zeigt eine Modellierung, in der die Klasse Schmuck bereits als abstrakt gekennzeichnet ist. Kursteilnehmer, die diese Aufgabe bearbeiten, werden das zunächst nicht so modellieren, sicherlich aber feststellen können, dass es keinen Sinn macht, die Klasse Schmuck zu instanziieren, da im Konstruktor der Klasse noch nicht entschieden werden kann, welches Objekt zur Repräsentation des Schmuckstücks erstellt werden soll. Sie beinhaltet also den Quellcode zum Auf- und Abschmücken, hat aber kein optisches Erscheinungsbild, so dass ein Objekt keinen Sinn macht. Die Referenz objekt der Klasse Schmuck kann als protected deklariert werden, damit in den Unterklassen ein Zugriff möglich ist. Alternativ kann eine Methode zum Setzen dieser Referenz hinzugefügt werden.
Der nächste Schritt besteht darin, dass den Schmuckstücken eine zusätzliche Animation hinzugefügt wird, die durch einen Mausklick angestoßen werden kann. Hierzu wird eine neue Methode in die (abstrakte) Klasse Schmuck eingeführt, die erst in den Unterklassen realisiert werden soll. Diese Methode ist abstrakt, da in der Klasse Schmuck lediglich die Signatur definiert werden kann. Die Modellierung sieht dann wie in Abbildung 9 gezeigt aus.
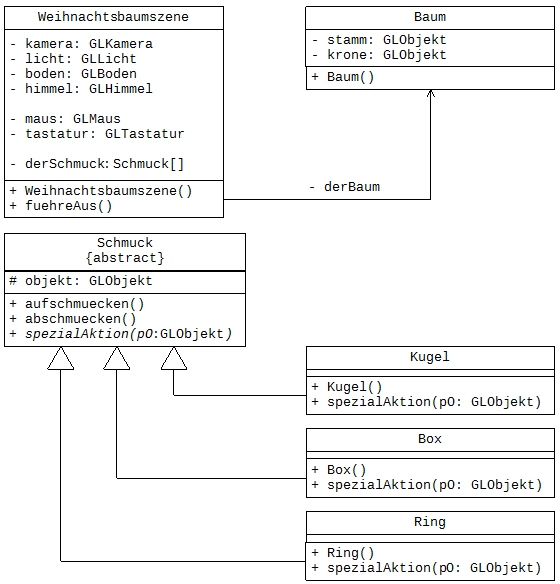
Abbildung 9: Modellierung der Weihnachtsbaumsimulation mit abstrakter Methode
In der Animationsschleife der Klasse Weihnachtsbaumszene wird mittels der GLOOP-Objektselektion das von der Maus angeklickte GLObjekt ermittelt und im Parameter der Methode spezialAktion an jedes Schmuckstück übergeben. In dieser Methode entscheidet jedes Schmuckstück, ob das übergebene GLObjekt jenes ist, mit dem es sich selbst optisch repräsentiert. Ist das der Fall, muss die jeweilige Spezialaktion in Form einer Animation durchgeführt werden. Die Hauptschleife der Klasse Weihnachtsbaumszene sieht dann wie folgt aus:

Quellcode
Welche Animation die jeweiligen Schmuckstücke beim Anklicken durchführen, ist für die Modellierung nicht von Relevanz. Ein Ring könnte sich einmal um sich selbst drehen, ein Päckchen die Farbe wechseln oder auch pulsieren. Eine Kugel könnte vom Baum fallen.
Dokumentation
Zur Dokumentation der GLOOP-Umgebung stehen drei Dokumente zur Verfügung.
Die Komplettdokumentation stellt die Funktionsweise der Bibliothek in all ihren Möglichkeiten umfassen dar und liefert auch Beispiele, wie Klassen und Methoden verwendet werden können.
Die Grundlagenübersicht und die Komplettübersicht sind als Nachschlagewerke zu verstehen. In der Grundlagenübersicht wird lediglich eine Übersicht über die wichtigsten Klassen und Methoden der GLOOP-Bibliothek gegeben, die im Anfangsunterricht benötigt werden. In der Komplettübersicht wird ein Überblick über alle Klassen und Methoden der Bibliothek gegeben.
Installation
Installationspakete
GLOOP Version 4.31 (Stand: Oktober 2023)
- Installationspaket für Windows (PDF, 4,28 MB)
- Installationspaket für MacOS (PDF, 4,28 MB)
- Installationspaket für Linux (PDF, 4,99 MB)
Installationsanleitung
Allgemeines
Um die Java-Bibliothek GLOOP verwenden zu können, müssen die folgenden Installationsschritte durchgeführt werden.
I. Das jeweils aktuelle Java Development Kit (JDK) muss installiert sein.
(z.B.: Download von Oracle)
II. Eine geeignete Java-Entwicklungsumgebung muss installiert sein. Zu empfehlen ist die Umgebung BlueJ.
(z.B.: Download von BlueJ)
III. Die Java Bindings for OpenGL (JOGL) Version 2.0 B.53 und die Java-Bibliothek GLOOP muss installiert sein. Beides ist in den obigen Installationspaketen enthalten.
Alle hier aufgeführten Produkte sind für die Verwendung in der Schule kostenlos und für alle gängigen Betriebssysteme zu erhalten.
Beispielinstallation
Das Java Development Kit (JDK) und die Umgebung BlueJ werden wie üblich installiert. Da beide Produkte über einen Installer verfügen, soll hier nicht weiter auf ihre Installation eingegangen werden.
Die Java Bindings for OpenGL (JOGL) und die Bibliothek GLOOP müssen per Hand installiert werden, was im Folgenden kurz erläutert wird.
Alle Jar-Dateien, die sich im Unterordner lib der obigen Installationspakete befinden, müssen in die Entwicklungsumgebung BlueJ eingebunden werden. Dazu können sie im Installationsverzeichnis von BlueJ in den Unterordner /lib/userlib kopiert werden. Alternativ ist es auch möglich, sie über die Einstellungen von BlueJ einzeln zu laden. Damit sind JOGL und GLOOP installiert. Ein Einbinden weiterer plattformabhängiger Dateien (z. B. DLL-Dateien unter Windows) ist ab GLOOP 3.4 nicht mehr nötig.
Wird in einem Projekt die Klasse GLTafel verwendet, so muss die Datei Zeichen.png in das jeweilige Projektverzeichnis kopiert werden. Es ist darauf zu achten, dass die aktuelle Datei dieses Installationspakets verwendet wird. Ältere Versionen der Zeichen.png führen unter Umständen zu fehlerhaften Darstellungen.
Anschließend sollte das GLOOP-System einsatzbereit sein.
Zur Verwendung der GLOOP-Bibliothek ist keine besonders leistungsstarke Hardware erforderlich. Man benötigt lediglich eine Grafikkarte, die den OpenGL 2.0 Standard unterstützt. Alle gängigen Grafikkarten unterstützen diesen Standard, auch ältere Modelle und Onboardkarten.
Die GLOOP-Bibliothek steht für Microsoft Windows, MacOS und Linux zur Verfügung.
Die GLOOP-Bibliothek kann in Schulen und sonstigen nichtkommerziellen Bildungseinrichtungen kostenlos genutzt werden. Näheres ist den Lizenzinformationen, die den Installationspaketen beiliegen, zu entnehmen.
In der Regel liegt es daran, dass kein aktueller Grafikkartentreiber installiert ist. Insbesondere die Standardtreiber des Betriebssystems bieten oft keine Hardwarebeschleunigung für OpenGL-Befehle.
Objekte vom Typ GLTastatur werden als Listener am Kamerafenster realisiert. Die Tastaturabfrage funktioniert daher nur, wenn das Kamerafenster den Fokus hat, was beim Programmstart nicht immer der Fall ist. Ein einfacher Linksklick mit der Maus in das Kamerafenster sollte das Problem beheben.
Ein Objekt vom Typ GLTafel verwendet die Bilddatei zeichen.png, um seine Aufschrift aus Teilen dieser Bilddatei zusammenzusetzen. Die Datei muss daher (wie eine Texturdatei) im aktuellen Projektverzeichnis gespeichert sein.
Manche Grafikkarten bzw. deren Treiber laden die Bilddatei zeichen.png auf dem Kopf, weswegen die falschen Zeichen ausgegeben werden. Eine kurzfristige Lösung ist, die Datei zeichen.png in einem Bildbearbeitungsprogramm zu laden und auf den Kopf zu stellen.
Die Bibliothek GLOOP befindet sich, ebenso wie dazugehörige Unterrichtsmaterialien, noch im Prozess der unterrichtlichen Erprobung.
Kommentare, Anregungen, Hinweise auf Unzulänglichkeiten und auch Fragen sind natürlich immer willkommen.
Ansprechpartner: Volker Quade (Autor der GLOOP-Bibliothek)
E-Mail an Volker Quade
Die Bibliothek GLOOP wird den mit Schule und Ausbildung befassten Institutionen und den darin Tätigen in NRW, also Lehrkräften, Referendarinnen und Referendaren, Lehramtsstudierenden, in der Lehrerausbildung Tätigen (z.B. Lehrende an Universitäten) sowie Schülerinnen und Schülern des Landes NRW zur Nutzung kostenlos zur Verfügung gestellt.
Eine kommerzielle Nutzung ist grundsätzlich ausgeschlossen. Abweichende Vereinbarungen bedürfen der Schriftform.
Haftungsauschluss
Für Schäden an Soft- oder Hardware oder Vermögensschäden, die durch das Benutzen des Programms entstehen, wird nicht gehaftet, es sei denn diese beruhen nachgewiesenermaßen auf einem grob fahrlässigen oder vorsätzlichen Handeln.
Autor der GLOOP-Bibliothek
Volker Quade